God, Symmetry and Beauty in Science II: A Personal Perspective

“Now, may our God be our hope. He Who made all things is better than all things. He Who made all beautiful things is more beautiful than all of them. …Learn to love the Creator in His creature and the Maker in what He has made.“(St.Augustine of Hippo, Commentary on Psalm 39).

“..and there is no doubt of the supreme mathematical beauty of Einstein’s general relativity.” (Roger Penrose,The Road to Reality).

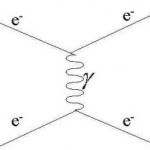
The Einstein field equation, shown above in abbreviated form, is considered by most physicists to exemplify the most beautiful of all physical theories, that of general relativity.  What are the requirements for a beautiful theory and how do these manifest, as St. Augustine has it, the Creator’s handiwork? The beauty is displayed in the mathematics of the theory, in the equations that relate it to the world.  A first requirement is generality/profundity–the equation has to be the basis for understanding a very broad and deep range of phenomena–as Einstein said,

“I want to know how God created this world. I am not interested in this or that phenomenon. I want to know His thoughts; the rest are details.“ (as quoted by A.Zee in “Fearful Symmetry”)

A second requirement is conciseness–what theoretical physicists would call elegance–Hemingway versus Faulkner or James. An equation that covers a page or so of symbols may be important and general, but it would not be beautiful. Much is summarized in the tensor notation of the general relativity field equations, but this beautiful form did not come easily.   It was not the result of sudden inspiration, unlike the lay view of how great science is done, but the result of eight years of dedicated effort, as Professor John Norton so well describes, in his discussion of Einstein’s notebooks: “General relativity was an achievement of creative imagination.”    

A page from Einstein's notebook on the formulation of general relativity--
see linke above to Prof. Norton's web-page

 There are other beautiful equations: Dirac’s equation combining quantum mechanics and special relativity, which led to the discovery of anti-matter and the theoretical basis for particle spin.    And it was Dirac who said “It is more important to have beauty in one’s equations than to have them  fit experiments”, a sentiment with which I am not entirely in agreement.

Dirac's Relativistic Equation for the Free Electron

In this connection, both the theory of general relativity and the Dirac equation have been confirmed experimentally.     General relativity was confirmed initially by the bending of light during a solar eclipse and by its quantitative explanation of the advance in the perhelion of the orbit of Mercury (as well as many other confirmatory experiments since then).
  The Dirac equation explained the existence of electron spin and predicted the existence of the positron (a positively charged electron), found experimentally some four years later. 

There is one other beautiful equation I want to mention, which in my opinion is as important as the two above: Boltzmann’s equation for entropy (S) in terms of thermodynamic probability (W), 

                                       S= k logarithm(W) 

(k is the Boltzmann constant).

Boltzmann's Tombstone;
the Equation  S= k logW
is at the top and the bust is of Boltzmann

This equation (engraved on his tombstone–see picture–and tattooed on my younger son’s arm) justifies the Second Law of Thermodynamics (the scientific version of Murphy’s Law: the universe is running down, no matter what 
                                           or, you can’t unscramble eggs without doing work), 
a physical law that, according to Einstein, will still be true many hundreds of years from now, even if all other theories are invalidated.

GOD, BEAUTY AND MATHEMATICS. 

Given that mathematics and mathematical physics have elements of beauty, what does this have to do with God?    The notion that mathematical truths are Divine is ancient history, going back to Pythagoras and Plato in ancient Greece. Augustine,  and more recently  Cantor (19th Century), argued that infinity is a manifestation of God’s ineffability.   
Why is science is explained mathematically? Or, as the renowned mathematical physicist, Eugene Wigner, puts it in his article, whence “The Unreasonable Effectiveness of Mathematics in the Natural Sciences"?  The question was, of course, answered some 500 years ago by Galileo: 

“The laws of nature are written by the hand of God in the language of mathematics.”


We want to understand the world and to recognize, as Scripture declares, that God looked on His Creation and saw that it was good. When you see children playing with toy cars or other objects and arranging them neatly in a line, you see the first beginnings of a desire for order and sequence.

Mathematics has an intrinsic beauty that is not constructed by our minds, but is discovered by us.   

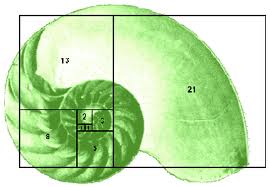Nautilus shell pattern illustrating the Fibonacci Sequence
(from "Heritage Math", by Savannah Morrow)

In nature, the pattern of sunflower florets, the nautilus shell, the growth of tree limbs is governed by the Fibonacci sequence,0,1,1,2,3,5,8,13… The rectangles combined from all the squares of the Fibonacci sequence have sides that have the “Golden Ratio” (“Golden Mean”), which the Greeks appreciated as beautiful proportion.    

 I want to emphasize that the beauty of pleasing proportion comes from more than symmetry.  Symmetry can be an element of beauty, but it neither a necessary element nor always a sufficient element.    It is the apprehension of order, an order that appeals to our intellect, that is the core of beauty.    This appeal to intellect distinguishes beauty from that which is simply good, according to St. Thomas Aquinas:

“The beautiful and the good are the same in the concrete existent (in subjecto), for they are based on the same thing, namely on the form.   For this reason the good is approvingly called the beautiful.  Yet, they differ in their intelligibility (ratione).  For the good appeals to the appetite; indeed, the good is what all desire.  So, it has the intelligible nature of an end, for appetite is sort of a motion toward a thing.   On the other hand, the beautiful appeals to the cognitive power:  for things that give pleasure when they are perceived (quae visa placent) are called beautiful. (emphasis added).   St. Thomas Aquinas,Summa Theologica

Aquinas also requires that which is beautiful be profound (he uses the term “large” or “big” but I think that can be construed as profound, as applied to beauty in science): “Beauty is found in a large body”.
I think Aquinas also shows the connection between Beauty and God in his Fourth Way, (the fourth of five ways of demonstrating the existence of God), which can be stated using the conclusion of the syllogism given in the link, “Thus, there is something that causes the being and goodness of every perfection in all things, and this is God.”

The "Big Trees" of Yosemite Park
(note the small size of the person
in the foreground.)

My own appreciation of the beauty of nature (I was too young and ignorant to realize the beauty of science) came as a teen-ager, going to the Griffith Park Planetarium in Los Angeles, and later, working one summer in the  Forest Service at Yosemite and seeing the Big Trees in their then unspoiled setting.
And all this became reinforced, later on when I became a Catholic (but more of that in a later blog) and saw that all of science was realized in Psalm 19a, “The Heavens declare the glory of God.”

Twitter

Facebook

Link










God, Symmetry and Beauty I: The Standard Model and the Higgs Boson.

In all things holy, we look for beauty.

“Tyger! Tyger! burning bright
In the forest of the night,
What immortal hand or eye
Could frame thy dreadful symmetry?”
William Blake.

“The mind of God appears to be abstract but not complicated.  He also appears to like group theory.”
Anthony Zee in “Fearful Symmetry”.

“You know what Aquinas says: The three things requisite for beauty are, integrity, a wholeness, symmetry and radiance.”   James Joyce in “Stephen Hero”

INTRODUCTION.

Flower Rosette for Bowed Psaltery
(Inspired Instruments)

In the previous blog, I decried the use of the term “God particle” applied to the Higgs boson and gave links to several columns that did likewise.   Nevertheless, finding the trail of a Higgs-like particle is an impressive (not to mention expensive) bit of science.   It is most impressive as the keystone of a beautiful structure, the “Standard Model”, an edifice built on the bricks and mortar of  group theory (the mathematics of symmetry) to explain the physics of fundamental particles.   To explain this, I’ll give a very brief account of how symmetry came to be an important theoretical tool in physics, and how it came to be an essential part of the Standard Model.   Now symmetry is not the only element of beauty in physical theories, but, as A. Zee demonstrates eloquently in his book about symmetry and physics, “Fearful Symmetry–The Search for Beauty in Modern Physics”, it is one on which theoretical physicists rely heavily:

“Fundamental physicists are sustained by the faith that ultimate design is suffused with symmetries.”

It is also true that beauty/elegance do not in themselves suffice to establish truth in science;  there has to be empirical verification for a theory in order for it be scientifically valid and useful, so we will show below how some beautiful theories were negated by experiment.   In our story the Higgs boson will not be the main character; rather it will (to switch analogies) be a coda to a symphony (as in Beethoven’s 8th).

SYMMETRY AND PHYSICS–INTRODUCTION

Celtic Knot Rosette for Bowed Psaltery
(Inspired Instruments)

In 1915 a German mathematician, Emmy Noether, discovered that two fundamental conservation laws of mechanics–the laws of conservation of linear momentum and of angular momentum–could be derived from symmetry considerations for related “action integrals”. What this amounts to, in simpler terms, is that there is an essential relation between the conservation of momentum and invariance under an appropriate symmetry operation–for example, for angular momentum, that the physical situation has the symmetry of a sphere, i.e. is invariant under rotations.   When I read about this in graduate school (way back when), I thought it was elegant and beautiful piece of work–to get a fundamental physical law from symmetry considerations alone–but  did not then appreciate the full scope of symmetry in physics.   At that time I thought symmetry (via the mathematical tool, group theory) was important only as an aid to simplifying solutions to problems,  showing what types of transitions were permitted between quantum states, but how wrong I was!

  A BRIEF HISTORY OF THE STANDARD MODEL: SYMMETRY = THEORY

In this short piece I can’t hope to give an adequate summary of the development of modern physics, the discovery of fundamental particles (or, as thought in the 1930′s and 40′s, what were thought to be fundamental), the electron, neutron, proton, positron, neutrino, photon.  For the reader who wants to read about this history and the development of the Standard Model in more detail, there are several good references:  “Fearful Symmetry” by A. Zee, “Not Even Wrong” by Peter Voit, “The Hunting of the Quark” by Peter Riordan, or “Deep Down Things” by Bruce Schumm.    There are articles in Wikipedia on particle physics and the Standard Model.

Triune Celtic Knot  Rosette for Bowed Psaltery
(Inspired Instruments)

My goal here is to show first, that the Standard Model resulted from the labor of many brilliant theoretical and experimental physicists, not all of whom are widely recognized as having contributed to this theoretical edifice, and second, that the resulting structure has all the qualities that physicists require for beauty in a theory:  elegance, universality and symmetry.   And, because it is a beautiful theory, simple yet profound, it displays again what St. Augustine said about the Creator, that all His work was beautiful:

“You, Lord, created heaven and earth.
They are beautiful because You are beauty.
They are good because You are goodness.
They exist because You are existence.”
Confessions, 11,4

SOME FUNDAMENTAL IDEAS.Before laying out a very brief account of the standard model and the Higgs field/boson, I want to give a qualitative explanation of some basic physical and mathematical concepts.   A fine account, which has a somewhat different emphasis than I will take, is given by a Dutch physicist, Marcel van Velzen

FIELD/FORCE PARTICLE EQUIVALENCE.  
Fields are essentially forces, varying in strength and direction through space.   The notion of a field was introduced back in the early part of the 19th century by Michael Faraday studying magnetic forces.   (See picture of the magnetic field–array of iron filings over a bar magnet).

Magnetic Field: Iron Filings over Bar Magnet

The electromagnetic field consists of electric and magnetic fields alternating in strength and direction like waves, propagating through space.     Light is in fact an electromagnetic field.   Now light can also (as Einstein first showed) behave as particles, photons.  This is an aspect of the “wave-particle” duality that lies at the heart of quantum mechanics.   Since charged particles (electrons, protons) interact via the electromagnetic field, they can also be thought to interact via the exchange of “virtual photons”, as illustrated below.

electon(e-) / electron(e-)
interaction via
virtual photon (gamma)

The same pattern of field/particle duality,  forces that can be represented as exchange of particles, exists for other fundamental interactions.   The four fundamental interactions are gravity, weak, electromagnetic and strong.  Gravity, as we all know, is the force that made the apple drop on Newton and that holds the planets in orbit around the sun.   The weak interaction is manifested in radioactive decay and is an essential mechanism for conversion of mass to energy in the sun.   The electromagnetic force, as explained above, is the long-range force between charged particles–it holds material objects together and enables a bat to impel a baseball over the fence.   The strong force holds nuclei together and, more fundamentally, contains the fundamental particles, quarks, inside protons, neutrons and higher mass mesons.    Leptons are fundamental particles other than quarks: electrons, positrons, muons, neutrinos;  leptons are not carriers of the fundamental interactions.  (See also “The Universe Adventure”.)  Quarks make up protons, neutrons and higher mass mesons.    What has been left out of the above is the Higgs field and its complementary particle, the Higgs boson, but more of that below.

SOME IDEAS ABOUT SYMMETRY.   
Symmetry has to do with sameness when things are rearranged or moved.    A good illustration of symmetry is shown by the inset figures of bowed psaltery rosettes:   if appropriate rotations (about axes perpendicular to the plane or in the plane) or mirror reflections are done, the rosettes will look the same.    Now there is another kind of symmetry important for particle physics, permutation symmetry.  Let’s consider identical triplets with labels 1,2,3 (see figure).    (The triplets aren’t quite identical, but let that  pass.)

Triplets (almost identical)

Suppose the babies are switched around in position and the labels removed–neglecting such distinguishing features as positions of legs, etc,(and parents’ special knowledge of distinguishing features);  then the total picture will look the same.    So the idea of permutation symmetry is that if we disregard arbitrary labels on otherwise indistinguishable objects, they  can be switched around in position and there will be no way to tell the difference between the original and the modified arrangement.

Mathematical tools for dealing with symmetry are given by group theory; I’ll try to list a few of the important ideas here and give a more detailed example below. A mathematical group is a collection of elements which obey particular multiplication rules (rules of successive operations).   The group is such that any multiplication gives one and only one member of the group, the group contains the identity element I (that is, multiplication by I is like multiplying by 1–it doesn’t change anything), and to each  element there is a corresponding inverse (multiplying successively by an element and its inverse gives the identity I).   Here’s an abstract, but simple example:  the elements I,A such that IxA = AxI =I  and AxA=I  (i.e. A is its own inverse).  The group would be realized (the math term for a concrete example) in the permutations of two identical objects labeled with the numbers 1 and 2,  and put in an order (1,2):  the identity I would be (1,2)–>(1,2), leaving the objects alone;   the element A would be (1,2)–>(2,1), interchanging the order of the objects. If we interchanged twice, AxA, we would get back to the original order, i.e. the identity operation, I. This group  would also be realized by symmetry operations on objects such as the capital letter Z (rotation by 180 degrees about an axis perpendicular to the plane).


One very important feature of group theory for the Standard Model is the notion of representations.    A representation is a collection of matrices which obey the same multiplication rules as the group. The size of the matrix (how many rows or columns) will correspond to the number of objects it acts on;  for example, a 3×3 matrix will act on three objects.


SYMMETRY AND PARTICLE PERIODIC TABLES.

I hope at least some of you remember from high school Chemistry how Mendelyev’s Periodic Table helped make sense of the order of elements and their chemical behavior. In a similar way one can arrange fundamental particles into symmetric tables, arrangements which turn out to be explained by group theory, in the same way that the chemical periodic table was explained by quantum mechanics.   Below is an example of such a table:

Quart Octer from Cronodon.com
(http://cronodon.com/Atomic/QCD.html)

The table represents the “Eight-fold Way” put forth by Gell-Man in the 60′s to explain the composition of baryons(composite heavy subatomic particles) in terms of quarks. The states (i.e. the fundamental particles) in this octet are each characterized by the same spin number, 1/2.   The u,d,s stand for the quark “flavors”, up, down and strange, respectively; n and p, are the two atomic particles, neutron and proton, respectively; the middle row is the sigma triplet  and the lamda singlet states.  Each row represents states (or particles) which are changed into each other (or into combinations) by operations of the SU(3) symmetry group.  As one moves down the Y-axis of the figure one increases the “strangeness” of the composite particle, i.e. increases the number of strange quarks in a given particle/state.   The superscripts -, 0 and + give the electric charge for each particle/state; these charge numbers can be found from the charges of the quarks composing each particle:  u quarks have a charge number +2/3,  d and s quarks – 1/3.  I want to emphasize that this octet is only a convenient way of viewing the particle/states, again, much as the periodic table helps us to think about atomic structure and chemical behavior.   Also, it is important to note that the symmetry of the three quarks is only approximate (like that of the triplets above), since the masses of u and d quarks differ slightly, and the strange quark, somewhat more.


What does all this have to do with group theory?   Group theory tells us that for a given symmetry, the dimensions of the various possible representations are fixed.  So, for example, for SU(3) symmetry there will be a representation of dimension 8 (as in the diagram above) which will have two doublet states (the n and p and the Chi – and Chi 0  rows) a triplet state (the Sigma -, 0, and + row) and a singlet state (the lambda 0 row). There would not be representations of dimensions 7 or 9,  for SU(3) symmetry, so that if a septet or nonet state were observed, that would belie an SU(3) symmetry.    For SU(3) symmetry there is also a representation of dimension 10, which is  realized below in the decuplet of very short-lived baryons (observed as “resonances” in particle physics) with total spin 3/2.

Baryon Decuplet (10-fold)

In this decuplet, each horizontal row increases in “strangeness”, the number of strange quarks in the composite particle/state:  the top row has 0, the second 1, down to the bottom (Omega) with three strange quarks.   The diagonal rows have the same electric charge: beginning at the left, -1, going to +2 for the Delta++ particle.   Each of these particle/states is more energetic and consequently more unstable–shorter lived–than corresponding particle/states in the octet (spin 1/2 states).   In fact, when the decuplet was proposed by Gell-Mann, the Omega- particle was predicted, but had not been observed; its finding was a dramatic confirmation of the theory.


GAUGE INVARIANCE SYMMETRY.

A critical and foundational element in contemporary physical theory is gauge invariance. Gauge invariance is a type of local symmetry, that is to say, symmetry is given at various points, but changes as you move.   The symmetry is not global, i.e. is not the same throughout the space (refer to the image below, taken from the Wikipedia article linked above):

Local twisting of up and down coordinates (Cartesian coordinates) to illustrate gauge invariance (taken from linked Wikipedia article). Note that gauge invariant theories (e.g. general relativity, quantum field theory) would be valid at each point, despite the twisting and stretching of the coordinate system.

Imposing gauge symmetry will greatly restrict the physics and yield carrier particle(s) for the fields:  for quantum electrodynamics (QED) theory, the photon results.   More general gauge invariant theories (e.g. Yang-Mills theory, see below), yield gauge bosons to carry the fields.   The term “gauge” came from Hermann Weyl in his 1915 work on gauge invariance in electromagnetic theory and relativity–he used the term to relate to “distance” and its changes (as, for example, the distance between railroad tracks).


SYMMETRY BREAKING  

An important notion in theoretical physics is that of symmetry breaking (follow the link in the heading above for a detailed explanation).  Here is a relatively simple example:  consider a drop of water (say, as a particle in mist), roughly spherical in shape and therefore highly symmetric; let the temperature fall to the freezing point and the drop will spontaneously turn into a snowflake (or an ice crystal) of lower symmetry.   Another example is that of an iron bar that at sufficiently low temperature becomes magnetized (all small magnetic domains in the bar line up in the same direction), giving a direction (that of the magnet N to S poles) and thereby lowering the symmetry (which prior to the magnetization did not have a specified direction).
Symmetry breaking plays a fundamental role in the Higgs field; it is the mechanism by which the Higgs field endows fundamental particles with mass. Symmetry breaking is depicted in the “Mexican Hat” potential shown below (a similar diagram was shown in Higgs’ original article proposing this potential and mechanism for symmetry breaking).

Mexican Hat Potential

Wine Bottle with Punt
(Hill at Bottom)

If you look at the Mexican Hat potential (so-called because it looks like a sombrero) and the wine bottle with the punt (the hill at the bottom) you’ll see that they have a circular symmetry.     Now consider what would happen if you put a small ball (very gently) into the center of a bottle without a punt, just a flat bottom.    It would stay in the bottom at the center and there would still be circular symmetry.   Now consider what would happen if you put the ball into the bottle with the punt, setting it at the top of the punt–it might stay, but that would be an unstable equilibrium, and the ball would most likely roll to the side of the bottle.  The circular symmetry would thereby be broken, because the position of the ball at the side of the bottle defines a unique direction.  The same thing will happen with the Mexican Hat (Higgs) potential.   A system at the top of the central hill will spontaneously descend to the lower energy at the rim, and thereby break the circular symmetry.


YANG-MILLS THEORY 

The cornerstone of the Standard Model is Yang-Mills theory.   The theory was proposed in 1954 by Chen Yang and Robert Mills as a generalization of gauge-invariant quantum electrodynamics, which had been remarkably successful.   The goal was to give a theory for the strong nuclear interaction.     However, the theory was not successful: it predicted the existence of massless carrier bosons (in addition to a photon), which were not observed.


THE HIGGS FIELD/BOSON 

The Higgs field was proposed by Peter Higgs in 1965 as a way to bring spontaneous symmetry breaking into Yang-Mills theory.   The Higgs field generates mass for particles in the following way, as nicely explained by Van Velzen (see link above).   Consider the fundamental property of mass, inertia:  according to Newton’s Laws of Motion:  a particle moving with constant velocity in a straight line will continue to move in a straight line unless acted on by a force;  if acted on by a force its velocity will change (acceleration will occur according to the famous equation F=ma).  Mass enters by requiring a force to change velocity (accelerate the particle), the force being proportional to mass for given acceleration.   If a particle does not have mass, it’s velocity will be constant, as is that of the massless photon, which has the speed c, the speed of light.    One can think of the Higgs field acting as a repulsive  lattice; that is, one can imagine a regular array of points, which are sources of equal repulsive forces.    Lattice points behind a particle will push the mass particle forward; lattice points in front of the mass particle will push it backward with equal force; the effect will then, as the diagram given by Van Velzen shows so well, be for the particle to move with constant velocity.   (Note: the explanation given by many popular accounts of the Higgs field, as if a particle were moving in a viscous fluid, is not correct;  if that were so then the particle would decelerate and stop moving).


ELECTROMAGNETISM+WEAK INTERACTION=”ELECTROWEAK” THEORY. Sheldon Glashow extended the Yang-Mills theory to cover both electromagnetism and the weak interaction (beta-decay) in 1960.   However, his theory was deficient in that it was not gauge-invariant;  the masses of the carrier  bosons were specified explicitly.  In 1967 Steven Weinberg and Abdus Salam independently proposed a truly gauge-invariant version of Glashow’s theory;  they achieved this by adding the Higgs field to the theory, thereby yielding spontaneous symmetry breaking with massive carrier bosons.  The theory was confirmed experimentally in 1973 by finding “neutral currents” in neutrino scattering and in 1983 by the detection of the carrier bosons, W and Z.     

QUANTUM CHROMODYNAMICS = “QCD”  
The next extension of Yang-Mills theory in the Standard Model was quantum chromodynamics, QCD, the theory to explain the strong interaction between quarks, the particle constituents of protons, neutrons and other heavy particles (baryons).   Glashow, Salam and Weinberg were jointly awarded the Nobel prize in 1979 for this theory.Experimental evidence strongly suggested the existence of three types of quarks, i.e. three types for each of the six different quark “flavors”–up, down, strange, top, bottom, charm;  the three types differ in a degree of freedom that is called color, but were otherwise identical in mass, charge, etc, (the quark color has no relation to colors observed in the ordinary world).  Thus there are “red”, “blue”, “green” up quarks, “red”, “blue”, “green” down quarks, etc., as shown in the illustration (from the Wikipedia article on Quarks linked above).  

Colors of Up (u) and Down (d) quarks in a proton

The quarks are bound within a baryon (nuclear or other heavy particle) by carrier bosons termed “gluons”.      A strange, but theoretically justified and experimentally verified  property of the force binding the quarks inside a baryon, is that the force becomes vanishingly small as the quarks get close to each other but becomes increasingly strong as they get distant, so that effectively the quarks are bound within a particle and can’t get out.   This latter behavior is called “quark confinement” and while models for it have been proposed (e.g. like the elastic force of a very strong rubber band), the exact mathematical justification is yet to be achieved.


GRAND UNIFICATION THEORY = “GUT” 
An obvious next step in the standard model is to give a theory in which electromagnetism, the weak interaction, the strong force and gravity are all derived from a common gauge theory, analogous to the derivation of electromagnetism and the weak interaction from the electroweak theory.    There were a number of attempts following the success of QCD to find a theory that would unify all various types of forces and interactions.   The first of these was given by Sheldon Glashow and Howard Georgi in 1974, who proposed a gauge invariant theory combining symmetries for electromagnetism, the weak, and the strong interactions.   Unfortunately the theory failed a crucial experimental test:  it predicted a much shorter decay rate for protons (by a factor of 100 to 10,000) than the lower limit determined experimentally.    Other proposed theories also fell short, and the attention of theoretical physicists turned to other “theories of everything” (TOE’s)–supersymmetry, string theory, M-theory–which I won’t discuss.

SUMMATION.

The Standard Model, while being a beautiful and coherent physical theory, does, nevertheless have deficiencies and problems. I won’t talk about these in detail here; Woit’s book, “Not Even Wrong” and the grand text by Roger Penrose, “The Road to Reality”, discuss these problems in more detail. You can also do a web search “Problems with the Standard Model” and find lots of sites; the problems listed in these sites overlap but do not all coincide.    In general, one can say that these problems are of a sort, “why?”–e.g. wherefore six flavors of quarks, or three generations of baryons;  why does the negative of the electron equal in magnitude the positive charge of the proton (fortunately, for the existence of the universe);  whence comes the violation of parity?     Nevertheless, the Standard model is an impressive structure.   To use an architectural analogy, the Standard model is an arch, the keystone of which is the Higgs field, and it rests on a foundation of basic theory.    Many scientists have contributed to the structure: to the foundation, Maupertuis, Noether, Weyl, with principles of least action, symmetry and conservation, and gauge invariance; to the arch itself, Glashow, Weinburg, Salam, and the many other theoretical physicists–Yang, Mills, Anderson, Wilson,t’Hooft, Veltman, Gross, Politzer, Wilczek–who contributed essential pieces to the theory.

Arch with Keystron--The Arch symbolizes the Standard Model
and the Keystone  Symbolizes the Higgs Field/Boson

And what does all this have to do with the title of this piece, God, Symmetry and Beauty? I’m going to leave that to a new piece. This has been a labor (in the child-bearing sense) much drawn-out and with great pain. As a colleague told me, the best way to learn about a subject is to teach it, and I have gone back to graduate quantum mechanics courses to review stuff I’d forgotten (not used in my research), gone to papers (Higgs original letter) to understand material that I had never needed or used, and thus have learned much.  I’m not sure whether more than the flavor (like those little spoonfuls at the ice cream store) has been conveyed, but those readers who do want to explore this topic in more depth should go to the books by Zee and Woit, and those links given in this paper.